|
|
||
|---|---|---|
| .. | ||
| README.md | ||
| magnitude-distribution.png | ||
| spacebook-magnitude-distribution.png | ||
| spacebook-original.py | ||
| spacebook.py | ||
README.md
SpaceBook
Category: Astronomy, Astrophysics, Astrometry, Astrodynamics, AAAA Points (final): 75 points Solves: 56
Hah, yeah we're going to do the hard part anyways! Glue all previous parts together by identifying these stars based on the provided catalog. Match the provided boresight refence vectors to the catalog refence vectors and tell us our attitude.
Note: The catalog format is unit vector (X,Y,Z) in a celestial reference frame and the magnitude (relative brightness)
Given files: spacebook-golf56788echo.tar.bz2
Write-up
by erin (barzamin).
SpaceBook is a very similar problem to Attitude Adjustment; we still need to solve an orthogonal Procrustes problem to align a set of stars to a catalog. However, we don't know which stars in the unknown set match to which stars in the catalog, unlike in Attitude Adjustment.
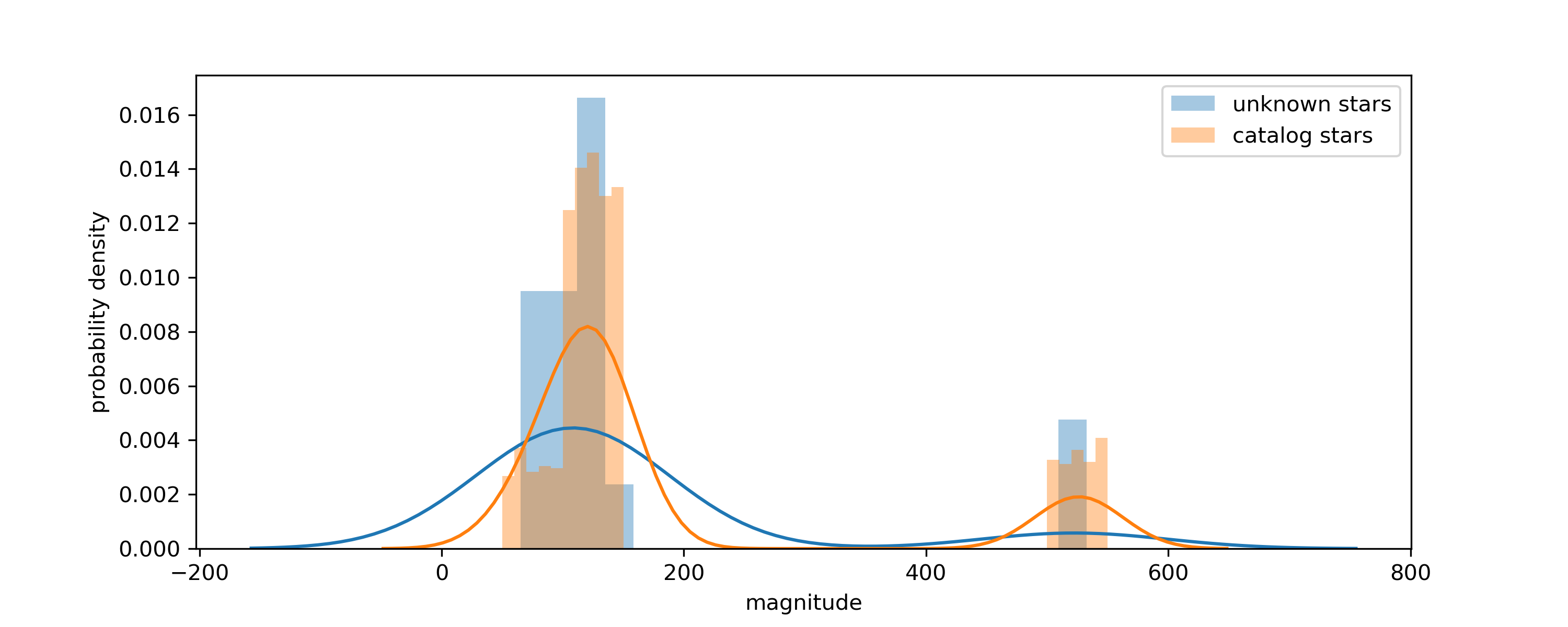
We're given a boresight vector \vec{v}\in\mathbb{R}^3 for each star, and a magnitude m. The vectors in the catalog set are off by some rotation from the vectors in the unknown set; the magnitudes match. Looking at the distribution of magnitudes, we see that there is a significant outlier population in both the catalog and reference sets, and that these outlier populations match:
My immediate suspicion was that we could take the outliers (simply by thresholding for stars with $m>500$) and, for each, directly match it to the catalog by finding the star with closest magnitude in the catalog:
refstars_magsorted = sorted(refstars, key=lambda x:x['m'])[::-1]
catalog_magnitudes = np.array([x['m'] for x in catalog])
matches = []
for idx, star in enumerate(refstars_magsorted):
if star['m'] <= 500:
break
match = np.argmin(np.abs(catalog_magnitudes-star['m']))
matches.append(match)
We can then align those brightest stars to their closest magnitude matches using the Kabsch algorithm:
P = np.vstack([x['v'] for x in [catalog[i] for i in matches]])
Q = np.vstack([x['v'] for x in refstars_magsorted[:4]])
print("rmsd: {}".format(calculate_rmsd.kabsch_rmsd(P,Q)))
rotation_mtx = calculate_rmsd.kabsch(P, Q)
rotation = Rotation.from_matrix(rotation_mtx)
Knowing the rotation, we can rotate all stars into the catalog reference frame and then evaluate
\arg\min_{\vec{u}\in\text{catalog}} \norm{\vec{u}-\vec{v}}_2for each unknown star with vector \vec{v} to find the closest star in the dictionary:
rotated = [dict(v=rotation.apply(x['v']), m=x['m']) for x in refstars_magsorted]
found_idxes = []
for star in rotated:
found_idxes.append(np.argmin([np.linalg.norm(star['v']-catalogstar['v']) for catalogstar in catalog]))
It's then trivial to send found_idxs back to the challenge as a comma-separated string of indices for each problem sent to us; the server happily sends us the flag after we answer its questions.
Full code